ΚΕΦ.8-Προσθέτω και αφαιρώ
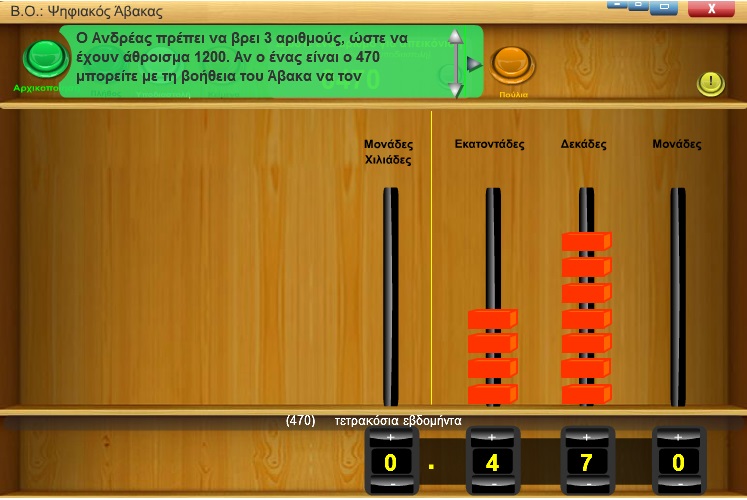
Πρόσθεση τριψήφιων αριθμών Εξασκούμαι στον ψηφιακό άβακα.
|
|
| ||||||||||||||||||
ΚΕΦ.9- Πολλαπλασιάζω με διάφορους τρόπους
1) 25 x 4 = (20 + 5) x 4 =(20 x 4) + (5 x 4) = 80 + 20 = 100
Αναλύω το 25 σε Μονάδες και Δεκάδες (20 + 5) και πολλαπλασιάζω χωριστά τις Δεκάδες και τις Μονάδες με το 4. Έπειτα προσθέτω τα γινόμενα.
Αναλύω το 25 σε Μονάδες και Δεκάδες (20 + 5) και πολλαπλασιάζω χωριστά τις Δεκάδες και τις Μονάδες με το 4. Έπειτα προσθέτω τα γινόμενα.
2) 34Χ10= 340 34Χ100=3400 34Χ1000=3400
Για να βρω το γινόμενο ενός ακέραιου αριθμού με το 10, το 100 ή το 1.000, γράφω τον αριθμό και συμπληρώνω στο τέλος τόσα μηδενικά, όσα έχει το 10, το 100 ή το 1.000.
Για να βρω το γινόμενο ενός ακέραιου αριθμού με το 10, το 100 ή το 1.000, γράφω τον αριθμό και συμπληρώνω στο τέλος τόσα μηδενικά, όσα έχει το 10, το 100 ή το 1.000.
|
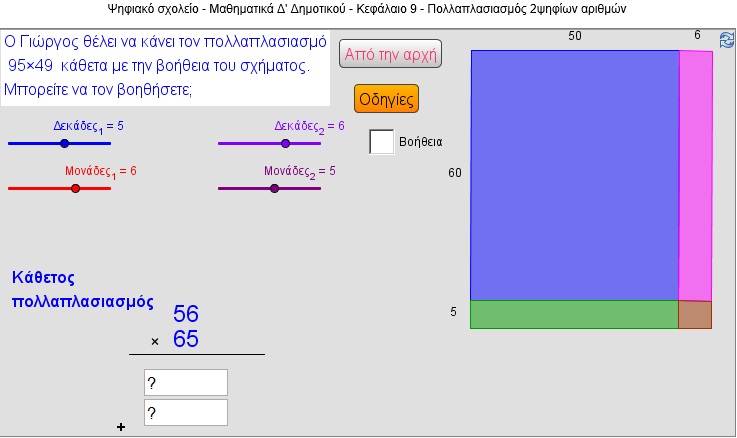
3) Αλγόριθμος του πολλαπλασιασμού (κάθετος πολλαπλασιασμός)
|
4) Οριζόντιος πολλαπλασιασμός (ελληνικός πολλαπλασιασμός)
Κάθετος πολλαπλασιασμός
| ||||||||||||||||||
ΚΕΦ.10- Επιλύω προβλήματα
|
| ||||||||||||
ΚΕΦ.11- Πολλαπλασιάζω και διαιρώ
|
|
| ||||||||||||||||||
ΚΕΦ.12 - Διαιρώ με διάφορους τρόπους
Θυμάμαι ότι: O πολλαπλασιασμός και η διαίρεση είναι πράξεις αντίστροφες.
Για να κάνω μια διαίρεση, πχ: 48:6= ;
Σκέφτομαι ποιο γινόμενο του 6 μου δίνει αποτέλεσμα πιο κοντά στο 48 χωρίς να το ξεπερνάει. Δηλαδή, με ποιον αριθμό πρέπει να πολλαπλασιάσω το 6 για να μου δίνει αριθμό ίσο ή μικρότερο του 48.
Σκέφτομαι την προπαίδεια του 6: 1x6=6, 2x6=12, 3x6=18, 4x6=24, 5x6=30, 6x6=36, 7x6=42, 8x6=48 !
Ωπ! 48! Άρα το 6 στο 48 χωράει 8 φορές! Συνεπώς γράφω: 48 : 6 = 8
Όμως κάποιες φορές μπορεί να περισσεύει κάτι..., πχ: 50:6=;
Σκέφτομαι ποιο γινόμενο του 6 μου δίνει αποτέλεσμα πιο κοντά στο 50 χωρίς να το ξεπερνάει. Δηλαδή, με ποιον αριθμό πρέπει να πολλαπλασιάσω το 6 για να μου δίνει αριθμό ίσο ή μικρότερο του 50.
Σκέφτομαι την προπαίδεια του 6: 1x6=6, 2x6=12, 3x6=18, 4x6=24, 5x6=30, 6x6=36, 7x6=42, 8x6=48 !, 9x6=54 !
Το 54 ξεπερνάει το 50, γι’ αυτό διαλέγω το 48 που είναι μικρότερο από το 50.
Άρα το 6 χωράει 8 φορές στο 50 (6x8=48) αλλά περισσεύουν και 2 (50-48=2). Συνεπώς γράφω: 50 = ( 6 x 8 ) + 2
Για τις διαιρέσεις Εκατοντάδων ή Χιλιάδων με το 100, γράφουμε τον αριθμό χωρίς τα δύο τελευταία του μηδενικά.
Π.χ.: 300 : 100 = 3 3.000 : 100 = 30
Για τις διαιρέσεις Χιλιάδων με το 1.000, γράφουμε τον αριθμό χωρίς τα τρία τελευταία του μηδενικά.
Π.χ.: 7.000 : 1.000 = 7
| ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΚΕΦ.12 | |
| File Size: | 71 kb |
| File Type: | doc |
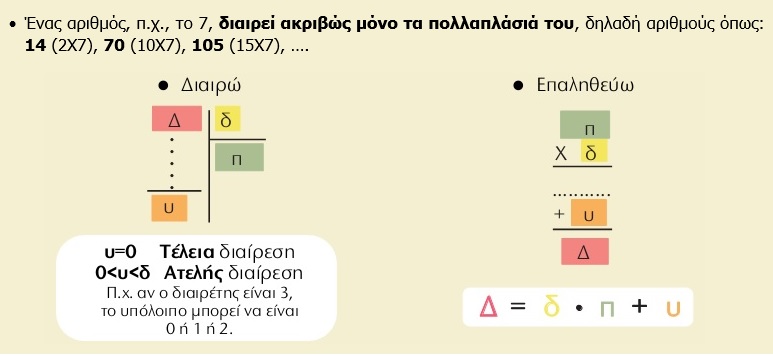
ΚΕΦ.13- Τέλεια και ατελής διαίρεση
ΚΕΦ.14- Διαχειρίζομαι προβλήματα
2η ΕΠΑΝΑΛΗΨΗ
|
|
|
|
| ||||||||||||||||||||||||||||||